Rydberg formula
The Rydberg formula, which was known empirically before Bohr's formula, is now in Bohr's theory seen as describing the energies of transitions or quantum jumps between one orbital energy level, and another. Bohr's formula gives the numerical value of the already-known and measured Rydberg's constant, but now in terms of more fundamental constants of nature, including the electron's charge and Planck's constant.When the electron gets moved from its original energy level to a higher one, it then jumps back each level till it comes to the original position, which results in a photon being emitted. Using the derived formula for the different 'energy' levels of hydrogen one may determine the 'wavelengths' of light that a hydrogen atom can emit.
The energy of a photon emitted by a hydrogen atom is given by the difference of two hydrogen energy levels:
Since the energy of a photon is
To apply to atoms with more than one electron, the Rydberg formula can be modified by replacing "Z" with "Z - b" or "n" with "n - b" where b is constant representing a screening effect due to the inner-shell and other electrons (see Electron shell and the later discussion of the "Shell Model of the Atom" below). This was established empirically before Bohr presented his model.
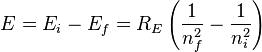


No comments:
Post a Comment